|
|
本帖最后由 hearts 于 2019-2-27 14:29 编辑
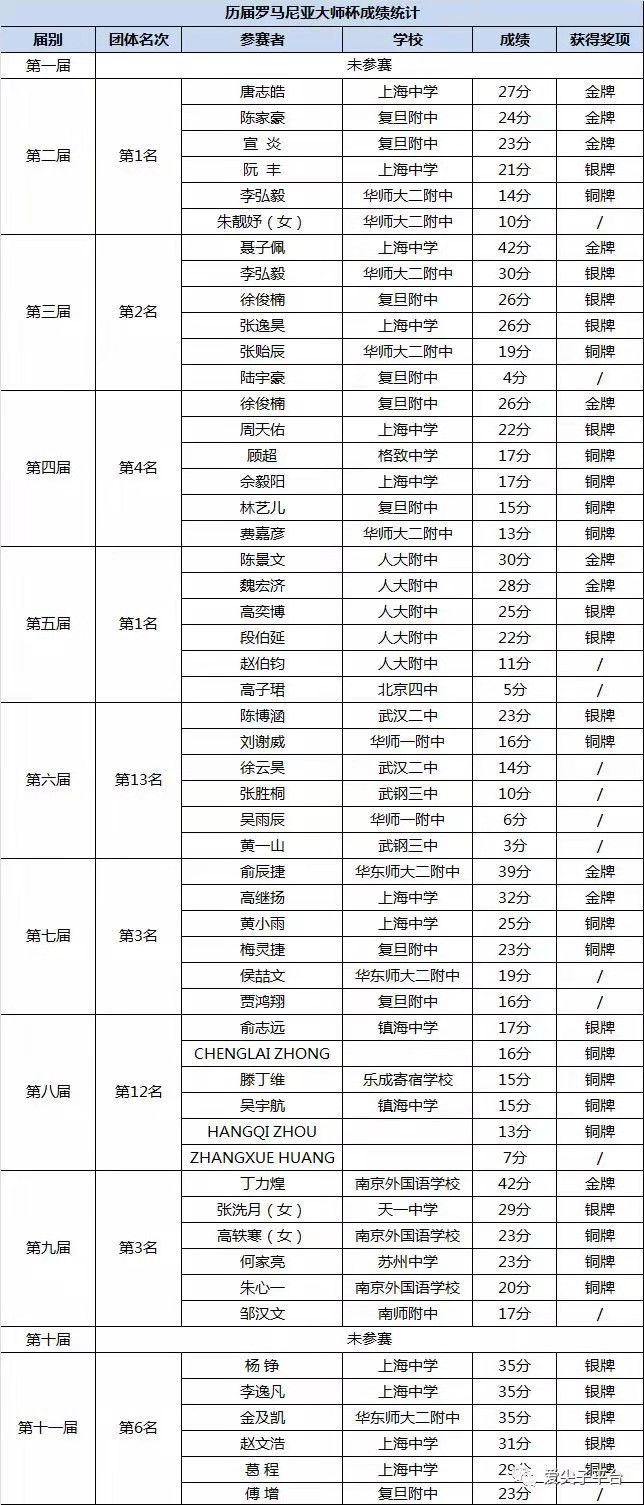
最近有些刷屏。上海代表队(都是集训队)代表中国去参加罗马尼亚大师赛,总分仅第六,最高分仅第15。
事实上观察一下就知道,上海队全部都失分在一道题上。而前7,8名这道题都是满分。如果加上这道题的得分,其实上海队最高分第一第二基本都会包揽(全满分)。
这道题是什么题呢?
Given any positive real number ε, prove that, for all but finitely many positive integers v, any graph on v vertices with at least (1 + ε)v edges has two distinct simple cycles of equal lengths. (Recall that the notion of a simple cycle does not allow repetition of vertices in a cycle.)
翻译一下,就是:
给定任何正实数ε,请证明 对所有的正整数v,除了有限个数(的v)之外,其他无限多(的v)都满足:任何具有v个顶点,至少(1+ε)v个边的图都拥有2个有相同长度的不同的简单圈。
学计算机的人都能看懂这道题。当然做出来是很难的。感觉可能上海队对计算机的离散数学和图论部分训练的不够,可能所有人都蒙圈了。
没学计算机的:这道题其实就是说,
给定任何正实数ε,请证明 对所有的正整数v,除了有限个数(的v)之外,其他无限多(的v)都满足:一共v个人,每个人都可以和其他人是朋友(或者不是),如果2个人是朋友,那么叫一个朋友对,在至少有(1+ε)v个朋友对的情况下,至少有2个朋友圈子(a-b是朋友对, b-c是朋友对,c-a是朋友对,叫做一个圈子,注意不是两两配对,而是一个线性循环配对)的朋友对数相同。
|
|






 发表于 2019-2-27 14:21
发表于 2019-2-27 14:21

 楼主
楼主
