本帖最后由 lllb 于 2021-8-16 16:36 编辑
数论不是必要的，如果不是喜欢+闲，没必要特地学。娃后半段对线代感兴趣了，进程中。 印象特深的一段：然而，迄今为止，数学中还有一大体系除了可以训练思维外没有任何实际应用，简直可以被光荣地授予“纯粹皇冠”了。这就是所谓的“数论”（这里指整数），数学中最古老的分支之一，也是纯数学思维最错综复杂的产物之一。 笑死，其实还是有用+好玩的，跟娃一起胡说八道很开心。 新内容我都带前几章，后面娃自习和做题。我以前没选修过数论，不了解的部分只在单位赶进度看看，回家再讨论，所以只总结小部分，暑假慢慢更新下。手上数论好材料不多，欢迎推荐。
《数论概论》比小蓝本更适合入门+讨论，小蓝本当题库不错。（讨论基础：具备初中基础知识和运算力；如果有高中的部分概念，更容易拓展。娃的基础：学过市北教材，做过尖子生夺冠整除部分，喜欢看数论相关的。上学期看过 科普名家名作院士讲数学那系列、数学美拾趣那个系列、素数的阴谋、费马大定理等介绍书籍，娃偶尔会说到跟分形也有关的蝴蝶效应。） 1.前三分之一难度不大，有很详细的引导。 2.课后题引导了很多后续概念的证明推导，引导兴趣很有效，可以说进度是不固定的、是可以控制在拓展里的。 3.书里每节都涉及到编程，娃还没学哎……某些手动计算了。 4.上学期看几何原本时，数论这章没开好头，经过这次长见识，倒是理解了几何原本里的数论章（类似辗转相除法的理解）。 作者很幽默。
娃一会儿写书上，一会儿写纸上，我粗略收集下。中间为了解决计算、证明，娃开了不少脑洞，吐了一些槽，还想办法学会了计算器的用法，让过程顺溜很多（毕竟我只给了很基础的计算器）。
一、数的基础讨论 前期介绍很通俗，从一些基本数的介绍出发，趣味性很足。  娃看到这里说她记得费马大定理，记录下  思考题有小部分不需要证明出来，是根据正文猜想。推导各类数之间的关联很有趣。比如计算同为三角数与平方数的数。 
娃乱七八糟小联想、小笔记挺多，说有些是以前数学科普书里看的，比如《素数的阴谋》等  比如拆解奇素数为平方和，娃还想出了个题，将奇素数因分成复数形式，发现能拆的都是模4余1的数（又可以结合平方数性质来解释），查了下都是高斯素数。（与后几章勾股数组的构造有关联了。）  二、勾股数组 是初始几章里很有意思的部分，构造数组的方式很多样。（最好有函数计算基础，对复平面、向量等有认识，拓展很有趣。） 1、通过分析奇偶，分析平方数性质，推导公式。 关于一组本原勾股数组（即互素的），里面必有2/3/5的倍数，正文里给出了2的证明方式。娃说很喜欢这步证明，跟醇香奶一样美妙，还补充写了在前一步就能完成证明（其他都是4的倍数，有一项却模4余2）。  课后题里，让证明3和5的倍数的情况：娃用平方数的性质，模3余1或0，来证明3的倍数；用平方的尾数（只有0.1.4.5.6.9等情况）组合，来证明5的倍数情况。  （后半题是用一种方法构造一组勾股数组。） 对比下：小蓝本（整除）提及的2、3、5的倍数性质，是作为单独练习题，糅合在同一题里证明完的。 
也是构造题（不知为啥还画了个乱乱小设计）  2、书里还用了函数＋固定坐标的方式推导勾股数组，但娃也用复平面和向量做了一样的构造结果。 
复平面法：第二题就是用的向量运算得出的勾股数组。（有次在店里玩，娃还拿小票背面出题为难爸爸，还自己写了答案纸，不过没画复平面。那天娃倒是给爷爷科普了一回虚数的几何意义，原来爷爷当年大学医学还没学过虚数、复平面。） 
三、辗转相除法 原本只用它求最大公因数GCD。这书给出了其与线性方程的证明和关联应用，原理讲得非常清楚，后面大量应用到。从这里开始完全是娃自习了，我在单位放了本中文版的，尽量同步看，有时没看就等回家听娃讲一讲。 先是求公因数 gcd
 简单的就做书上了
然后是用于线性方程。（二元一次不定方程，求出一组解后列通解） 
有时候字有够乱的……部分摘到草稿纸里做。
爷爷友情提供了好多草稿纸
比较了一下奥精、小蓝本的不定方程求整数解，第一组解多半是用尝试法（枚举法），再出通解，普遍性上差一点点，遇到较大数可能会很难凑。  正文学了解二元方程，课后题出了三元的，一开始，我让娃想个通解模式，她还尝试摸了套公式（一拍脑袋就写了，挺好玩，逻辑自洽了，也判断了有公因数的关联，做能做，但凑数还是一样麻烦） 后来福至心灵想起来可以拆成两组分别用辗转法出通解。（小傻子还很高兴，说发现一次不定方程的全解法啦哈哈，给她看了网上有人写的论文23333，人家早就知道了）  之后多元一次不定方程就普遍能解了，包括判定有无整数解。 
从小蓝本摘了点题做。
（部分内容跟小学初中很像，就当复习了） 
四、同余、费马小定理、欧拉φ相关 娃原来在尖子生系列的整除中学到过同余，倒是一直用得很溜，估计小孩都喜欢这类精简、偷懒的法子。 
同余式解决还是会用到辗转法哦
还写错词……（本来是列一下费马小定理的证明） 
后来看到欧拉φ定理的证明，说方式与费马小定理一致，还吐槽来着。
求φ值时，说书里用的是代入的归纳法，自己写了个因分的推导模式，不过最后还是归纳法。
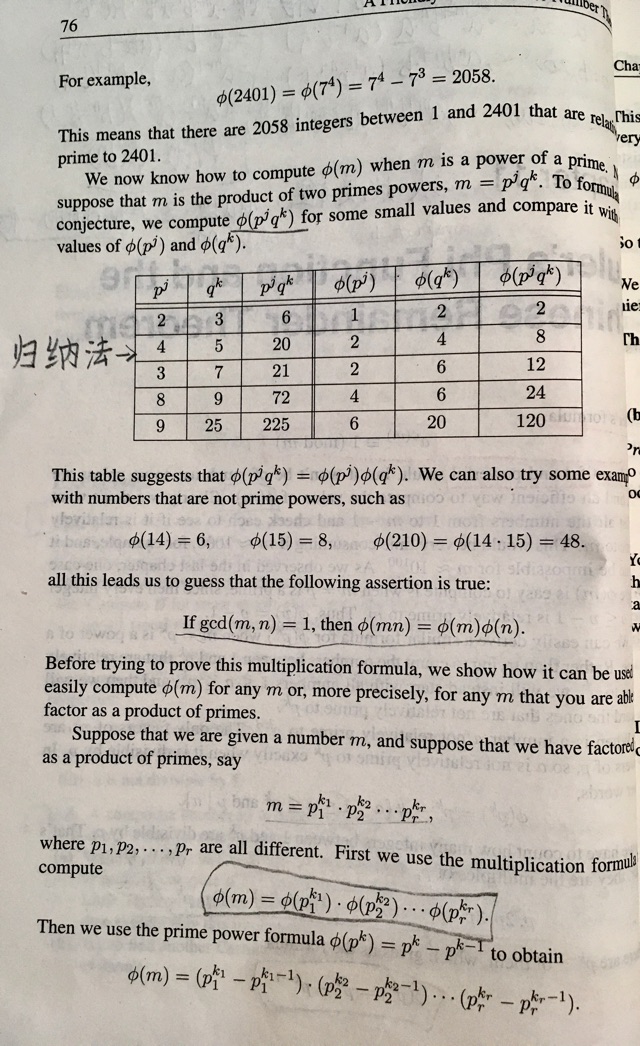
这里φ值翻来覆去地求解/倒推/z证明很好玩。
有些题目里要求推五种，娃倒很耐心地推很多、推十来个。
这题本来是求1-9每个数字的1000次的末四位数，就相当于求 mod 10000。娃开始还试探了下能不能用欧拉φ，结果还是用了逐次平方法，需要几次就拆为二进制数的组合。从这题开始熟练使用计算器揿平方找尾数了2333，发现规律非常有趣。（只要算出素数的那些，合数可以由素数的对应次幂得出。）
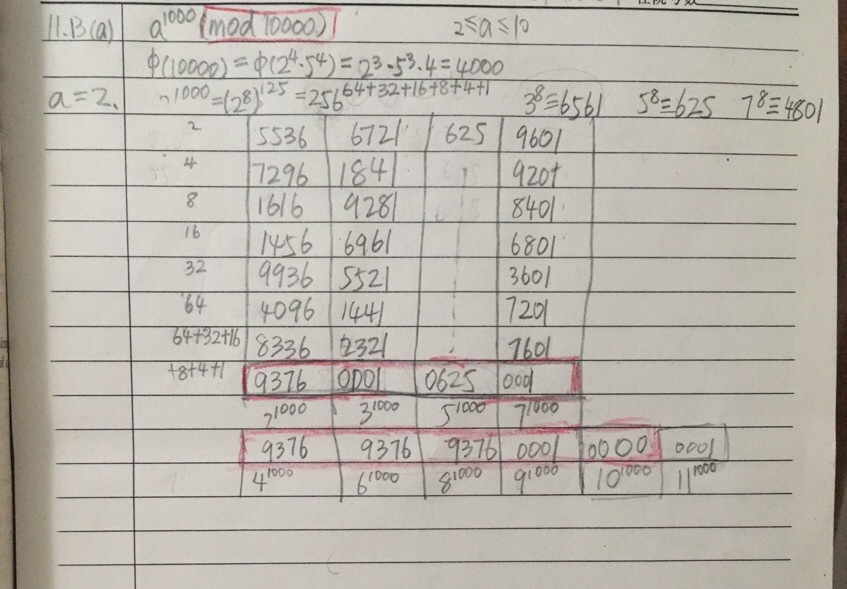
期间我在网上摘了点题，另外考娃。
不得不说，用到同余规则的地方都反应比较快。
结果娃还说自己总结了点规律（乱来的）
五、素数介绍章，不过主要在后面章节开展
完美数部分，题目做着做着还会画漫画小人23333不注意还真没发现
六、密码学相关
好像从十几章开始都跟密码学有关，这就到她感兴趣的部分了。
这题解码解得蛮逗的，过程中有一步是用辗转法解次数关联的线性方程，娃把正负号搞反了，悲剧啊，本来只要两位数次方的，变成要算六千多次。更没想到的是居然很有毅力地一路算到了，然后解出的码毫无意义。（算二进制数次幂模时，她都检查确认了，怎么就没在辗转法里检查符号呢，小孩好嫩2333）  尽管这样，我还是很感动的，这多繁琐啊，还能坚持下来。我跟娃爸都试着揿了揿计算器，马上泪奔了（毕竟只给了娃一只基础计算器）。当然二进制数的次方也不是白算的，能用上一部分。接下来一张就正本清源，算对了。解码为Fermat。好像是这次被我俩大夸特夸，觉得很有趣，后面几天还编了好几句密码考大人（编码解码的步骤一样繁琐）orz  特别夸一下娃想出的流畅的计算器揿法（①揿 “某数”“x”“ =” 可算该数平方；按"-""某数"，再持续按"="，会连减该数），比如揿出2604的平方，为七位数，娃就先连减7081的百倍，再连减其十倍，再连减7081，直到剩余数；接着余数平方，再如上做连减。这样可以连贯揿，而不用每步都记录来记录去求整数倍。娃不会编程，也有其他的收获，起码是动脑解决麻烦了。 数码表对应如图  我断断续续跟进度的，后面的还没拍，待补充整理。 PS：陆续看到有个别题目里的小分题是奥数里出现过的。
线代另开一帖了，估摸着假期能看完一轮。之后再继续看数论。
| 
发表于 2021-7-19 19:55
楼主
，刚刚翻了楼主的帖子，好多有趣的书。可惜最想看初心的数学那篇看不了。楼主能发新帖子吗？感谢
